Target Sum

Posted on |

问题描述（难度中等-494）

You are given a list of non-negative integers, a1, a2, …, an, and a target, S. Now you have 2 symbols + and -. For each integer, you should choose one from + and - as its new symbol.

Find out how many ways to assign symbols to make sum of integers equal to target S.

Example 1:

1
2
3
4
5
6
7
8
9
10
11
Input: nums is [1, 1, 1, 1, 1], S is 3. 
Output: 5
Explanation: 

-1+1+1+1+1 = 3
+1-1+1+1+1 = 3
+1+1-1+1+1 = 3
+1+1+1-1+1 = 3
+1+1+1+1-1 = 3

There are 5 ways to assign symbols to make the sum of nums be target 3.

Note:

  1. The length of the given array is positive and will not exceed 20.
  2. The sum of elements in the given array will not exceed 1000.
  3. Your output answer is guaranteed to be fitted in a 32-bit integer.

方法一：Using Recursive

通过递归，递归有重复的子结构。可以通过DP改善。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
package P494;

/**
 * 递归解决O(N^2)
 */
class Solution {
    private int[] nums;
    public int findTargetSumWays(int[] nums, int S) {
        this.nums=nums;
        return findTargetSumWaysIndex(nums.length-1,S);
    }
    public int findTargetSumWaysIndex(int index,int S){
        if (index==0) {
            if (nums[index]==0 && S==0) {
                return 2;
            }
            return Math.abs(S)==Math.abs(nums[index])?1:0;
        }
        return findTargetSumWaysIndex(index-1,S-nums[index])+findTargetSumWaysIndex(index-1,S+nums[index]);
    }

    public static void main(String[] args) {
        int[] ints={0,0,0,0,0,0,0,0,1};
        new Solution().findTargetSumWays(ints,1);
    }
}

方法二：Using DP

通过dp规避重复子问题。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
package P494;

/**
 * @autor yeqiaozhu.
 * @date 2019-10-14
 */
public class UsingDPSolution {
    public int findTargetSumWays(int[] nums, int s) {
        int sum = 0;
        for(int i: nums) sum+=i;
        if(s>sum || s<-sum) return 0;
        int[] dp = new int[2*sum+1];
        dp[0+sum] = 1;
        for(int i = 0; i<nums.length; i++){
            int[] next = new int[2*sum+1];
            for(int k = 0; k<2*sum+1; k++){
                if(dp[k]!=0){
                    next[k + nums[i]] += dp[k];
                    next[k - nums[i]] += dp[k];
                }
            }
            dp = next;
        }
        return dp[sum+s];
    }

    public static void main(String[] args) {
        int[] ints={0,0,0,0,0,0,0,0,1};


        int[] ints1={1, 1, 1, 1, 1};
        System.out.println(new UsingDPSolution().findTargetSumWays(ints,1));
        System.out.println(new UsingDPSolution().findTargetSumWays(ints1,3));
    }
}

对应的存储结构图：

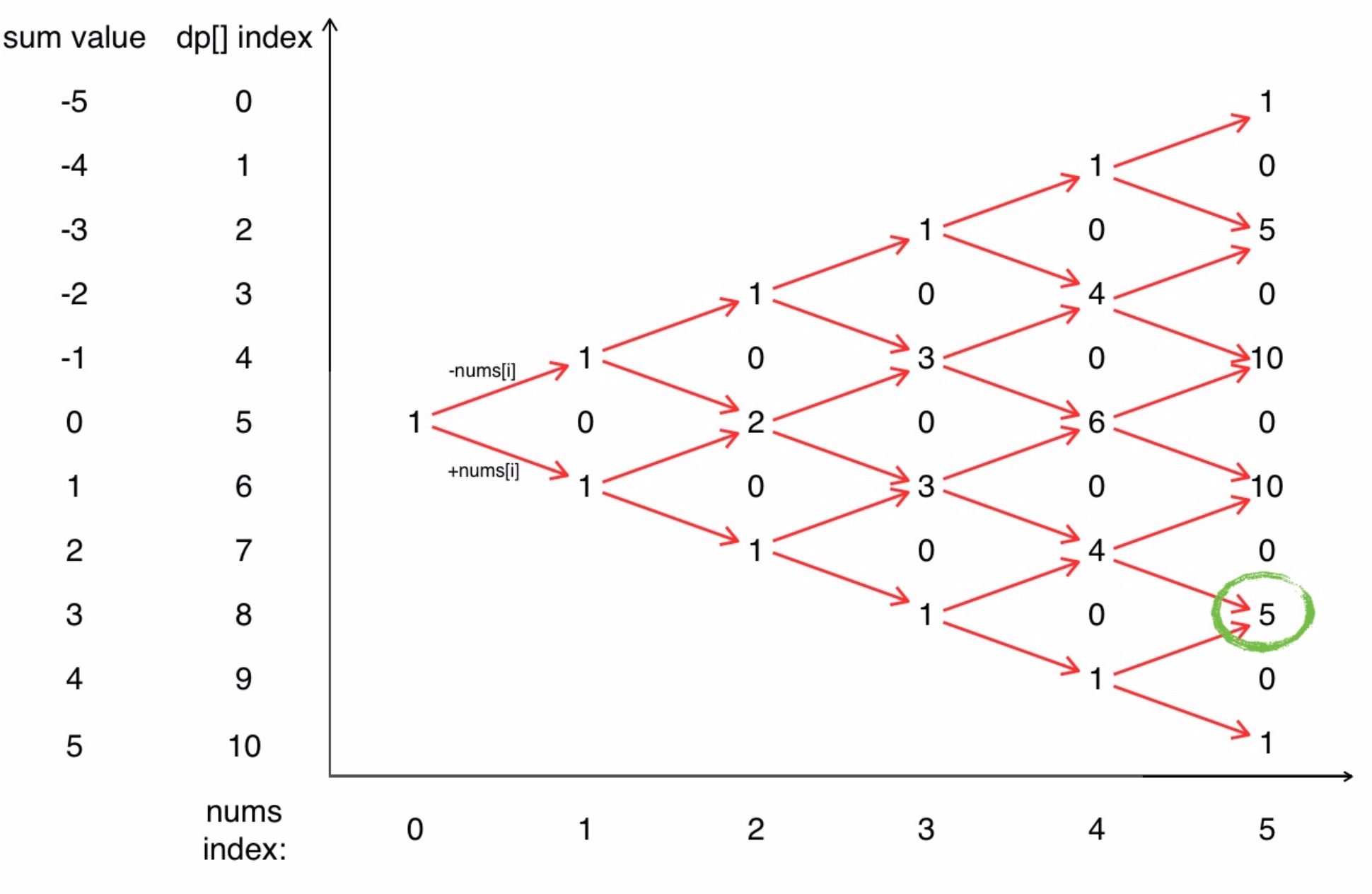
cmd-markdown-logo

方法三：Using DFS

回溯可以通过递归的方式去实现。这里通过map保存下重复的运算。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
public class Solution {
    public int findTargetSumWays(int[] nums, int S) {
        if (nums == null || nums.length == 0){
            return 0;
        }
        return helper(nums, 0, 0, S, new HashMap<>());
    }
    private int helper(int[] nums, int index, int sum, int S, Map<String, Integer> map){
        String encodeString = index + "->" + sum;
        if (map.containsKey(encodeString)){
            return map.get(encodeString);
        }
        if (index == nums.length){
            if (sum == S){
                return 1;
            }else {
                return 0;
            }
        }
        int curNum = nums[index];
        int add = helper(nums, index + 1, sum - curNum, S, map);
        int minus = helper(nums, index + 1, sum + curNum, S, map);
        map.put(encodeString, add + minus);
        return add + minus;
    }
}